Introduction

In this article, we are going to discuss merge sort..

All sorting algorithms - 1 ( Bubble sort, Insertion Sort, Selection Sort )

NOTE: Before discussing this algorithm, let me make clear that you should have some basic knowledge of RECURSION.

Merge Sort

This algorithm is also called as Divide and Merge algorithm.

In this algorithm, we divide the array in half, and we keep on dividing the array until we have an array, in which there is only a single element. Then we combine the array again in a sorted manner. See the below diagram to visualize what I just said.

In the above diagram, you can see that we had an unsorted array. Then we kept dividing the array until we were left with a single-element array. Then we traversed back and combined the array again in a sorted manner.

Let's look at pseudo-code:

merge_sort( arr, low, high ) {
    if(low == high ) {
        return;
    }

    int mid = (low + high) / 2;
    merge_sort(arr , low, mid );  // dividing the array
    merge_sort(arr, mid+1, high ); // dividing the array
    merge(arr, low, mid , high ); // merging back the array
}

merge( arr, low, mid, high ) {
    temp arrayList; // creating an arraylist
    int left = low;
    int right = mid+1;

    while( low<= mid && right <= high ){
        if(arr[left] < arr[right] ) {
                temp.push(arr[left]);
                left++;
        }   
        else {
                temp.push(arr[right]);
                 right++;
        }
    }

    // if their is a situation that one of the array is greter than the
    // the other array we can use simple while loops to traverse in the 
    // array and store the elements in the original array.

    while( left <= mid ) {
        temp.push(arr[left]);
        left++;
    }    

    while( right >= mid ) {
        temp.push(arr[right]);    
        right--;
    }    

}

Yes, yes I know the pseudo-code is a little too overwhelming.

So, let's try to understand this with an example.

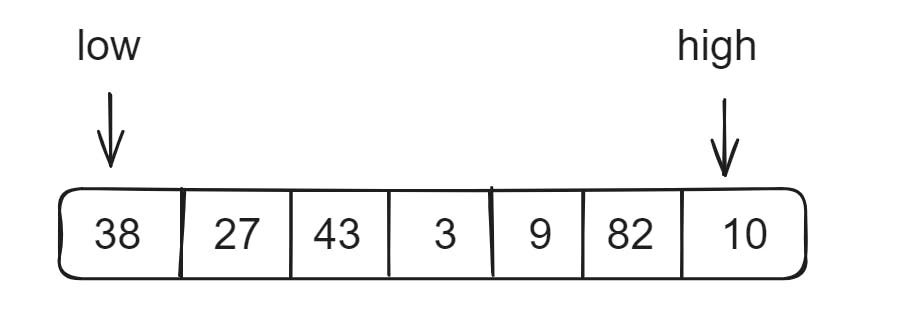
Let's take this array, for example, with a low pointer pointing at the first index and a high pointer pointing at the last index.

We enter into the merge_sort function, and first we check out the base condition if it is true or false. Since it is false, we go further.

Now we calculate our mid pointer by int mid = (low + high) / 2; , so here our mid the pointer will be, so we simply call the merge sort function again, we call the function, and we pass low as same but at high we pass the mid pointer. So we get a new array, divided into half.

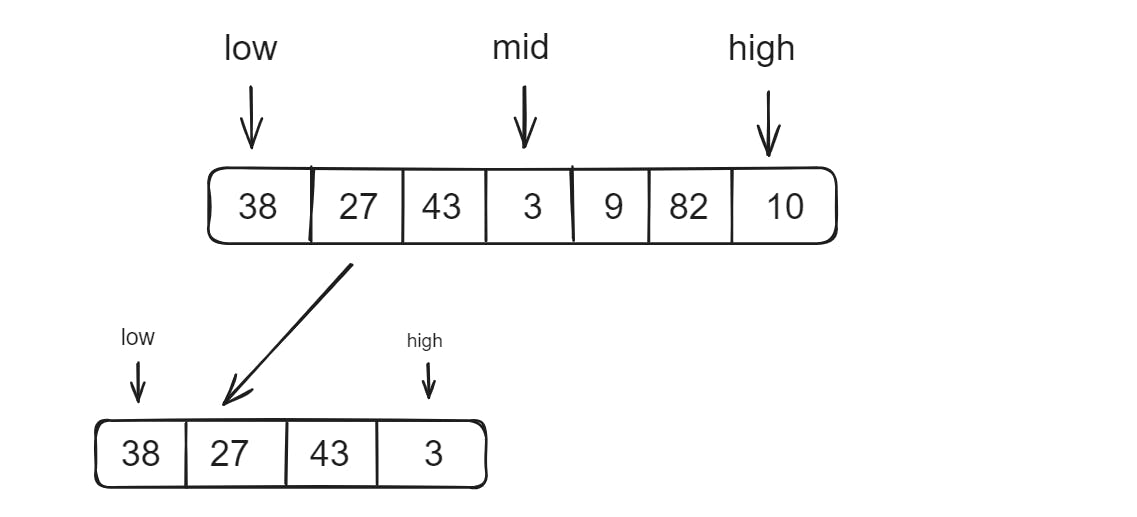
Now again, we go on to divide the new array further, and we keep on dividing until we are left with just one element at the end.

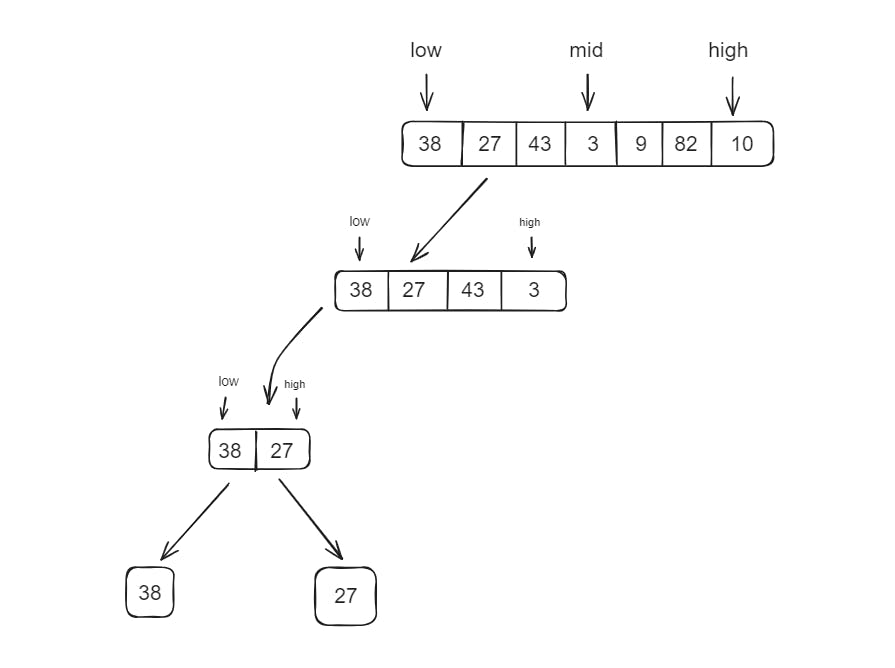
Now this is how the whole structure will look at the end.

NOTE: first the left part is sorted and then the right part of the subarray is sorted. This is the reason why in the diagram I am only showing you the left part of the array.

Now when you are only left with one single element in the array, the base condition executes:

if(low == high ) { return; }

Then we travel back in the array combining both the arrays together in a sorted manner.

To combine both arrays in a sorted manner we would use the merge function shown in the pseudo-code.

And voilaa! This is the simple merge sort algorithm.